Statistik Ceria
Official Statistics
Official Statistics adalah istilah di dunia perstatistikan yang sering digunakan dalam menyebut ukuran-ukuran statistik standard Internasi...
Programming in R dan RStudio
Introductions Salah satu keuntungan utama menggunakan R environtment (http://cran.at.r-project.org) adalah memudahkan pengguna menulis p...
Contoh Soal Uji Chi Square Kasus Satu Sampel Dilengkapi Penjelasan [Video]
Misalkan dalam pilkada Jakarta, calon gubernur nomor urut 1 ingin mengetahui proposri orang yang mendukungnya di 7 kelurahan di jakarta. Di...
[Video] Latihan Soal Uji Chi Square Dua Sampel Independen Dengan Penjelasan
Uji Chi square adalah sebuah teknik pengujian yang dapat digunakan untuk menguji apakah frekuensi yang diamati cukup mendekati frekuensi ya...
Metode Stochastic Frontier Analisis Untuk Menghitung Nilai Produktifitas
Stochastic Frontier analysis merupakan salah satu metode yang dapat digunakan untuk mengestimasi produksi. Metode ini sangat cocok bagi Anda...
Metode Newton Raphson
Andira Ika Nugraheni
Pada analisis regresi logistik biner, p ersamaan likelihood yang didapat adalah: Persamaan di atas merupaka...
[TUTORIAL] Cara Mendeteksi Autokorelasi Menggunakan SPSS
Andira Ika Nugraheni
[TUTORIAL] Cara Mendeteksi Autokorelasi Menggunakan SPSS Langkah-langkah : 1. Entry data ke SPSS Dalam hal ini X 1 = Motivasi...
Subscribe to:
Posts (Atom)


![Contoh Soal Uji Chi Square Kasus Satu Sampel Dilengkapi Penjelasan [Video] thumbnail](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjae3tfo7RK6QcKonIBULZUifiR4j18IJqRpZ2CHzc4ytNCUwym3PdZKNx4DIiPNO9ITgKUSu8TnOqrfAnj_jr1uSuQrCnyoa_LGxvCWIidVFUxwpqMYLYVdUFL6I0Kn2NhG87jaErPEac/s72-c/Uji+Chi+Square+-+statmat.id.png)
![[Video] Latihan Soal Uji Chi Square Dua Sampel Independen Dengan Penjelasan thumbnail](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhiPpUwpq1ofBCsT6Jm-RjHuTQ6ZTlpwVOuYmra30E9sgItsehM6ec1Iv6QLY4E7bXWuhtKFbLugL_wBKYBWddxxEj20fC36N1A5o6PEcZzloKUq7tZ-bIAsRaI6vul5wqlGXet2pPtyag/s72-c/Uji+Chi+Square.png)
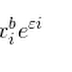

![[TUTORIAL] Cara Mendeteksi Autokorelasi Menggunakan SPSS thumbnail](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjj5H8I7Du44py4ro9IPpl2NkQjW3FZiz0tyt9rX7TnOR4tdtp0dO7hyphenhyphen2nrK_GZi4gqkL1OupA2rvWla9Sa9H3uCx2p8tYF1KtWXkMI_mffypeTCR2NMVWc5EbV51mJmuy4tXbAF5FdOSvC/s72-c/1.png)




