[Tutorial Excel] Analisis Ragam / Analysis of variance (Anova) dua arah tanpa interaksi

Dalam penyelesaian Analisis Ragam / Analysis of variance (Anova)  dua arah tanpa interaksi dengan menggunakan software tidak bisa digunakan SPSS. Sehingga perlu mencari software. Salah satu software yang bisa digunakan Microsoft excel. Walaupun tujuannya microsft excel bukan untuk pengujian statistik. tapi untuk yang sederhana bisa salah satunya anova dua arah tanpa interaksi. Contoh kasus yang digunakan sama dengan pengerjaan secara manual agar bisa dibandingkan apakah sama.

Contoh Kasus Anova dua arah tanpa interaksi:

Terdapat 4 metode diet dan 3 golongan usia peserta program diet Berikut data rata-rata penurunan berat peserta keempat metode dalam tiga kelompok umur.

Umur	Penurunan Berat Badan (Kg)				Total Baris
	Metode 1	Metode 2	Metode 3	Metode 4
< 20 tahun	5	6	2	3	T1* = 16
20-40	2	7	5	3	T2* = 17
> 40 tahun	7	3	4	3	T3* = 17
Total Kolom	T*1 = 14	T*2 = 16	T*3 = 11	T*4 = 9	Total T** = 50

Berdasarkan gambat tersebut terlihat bahwa setiap metode memiliki perlakuan yang sama sehingga bisa dikatakan ada hubungan dua arah. tapi tidak ada interaksi. Ujilah pendapat yang menyatakan bahwa keempat metode diet dalam ketiga kelompok umur memberikan rata-rata penurunan berat badan yang sama.
Buktikan jawaban saudara dengan pengujian varians, dengan tingkat nyata = 1 %

Solusi kasus Anova dua arah tanpa interaksi

Identifikasi Metode statistik yang digunakan

Pertama. berdasarkan hipotesis yang digunakan yaitu membandingkan rata-rata lebih dari dua kelompok maka metode yang mungkin adalah Anova. kedua Sampel yang digunakan tiap kelompok sudah dikategorikan sehingga tipe anova yang cocok adalah Anova dua arah. kemudian dari tiap kategori tersebut tidak ada pengulangan sehingga kita menggunakan anova dua arah tanpa interaksi.

Dalam metode anova yang perlu diperhatikan ada empat. asumsi normal dan homogenita santar varians kelompok harus terpenuhi. dalam contoh ini kita asumsikan asumsi terpenuhi karena kita fokus pada langkah-langkah anova satu arah. kemudian kelompok yang dianalisis berasal dari kelompok saling bebas. dan data yang digunakan merupakan data rasio. Setelah asumsi ini terpenuhi maka bisa lanjut ke perhitungan selanjutnya. kalau tidak ganti metode.

Pada anova dua arah tanpa interaksi terdapat dua hipotesis yang digunakan:

• Hipotesis anova kolom
  H0: μ*1 = μ*2 = μ*3, Tidak ada perbedaan yang nyata antara rata-rata hitung dari kategori Metode
  H1: μ*1 ≠ μ*2 ≠ μ*3, Ada perbedaan yang nyata antara rata-rata hitung dari kategori Metode
• Hipotesis anova baris
  H0: μ1* = μ2* = μ3*, Tidak ada perbedaan yang nyata antara rata-rata hitung dari kategori kelompok umur
  H1: μ1* ≠ μ2* ≠ μ3*, Ada perbedaan yang nyata antara rata-rata hitung dari kategori Kelompok umur

Langkah-langkah dalam uji hipotesis anova dua arah tanpa interaksi

1. Masukkan/import data ke SPSS, caranya yaitu buat data seperti kotak yang terdiri dari baris dan kolom. artinya setiap kolom dan baris menunjukkan kelompok. bingung menjelaskannya, Untuk jelasnya lihat gambar berikut:
   
2. Kemudian pilih Data, terus klik Data analysis. untuk data analysis ini tidak muncul default dalam excel. jadi perlu dimunculkan terlebih dahulu.  Untuk langkah-langkah mengaktifkan toolpak silahkan klik toolpak analysis. Maka akan muncul tampilan seperti berikut.
   
3. Kemudian pilih Anova two factor without replacement. maka akan muncul tampilan seperti berikut.
   
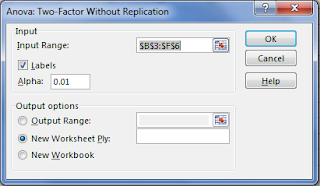
4. Pada Input range diklik maka akan muncul pilihan untuk memilih data. Pemilihan data dengan cara blok datanya mulai dari label sampai semua datanya, seperti pada data diatas semuanya diblok. Kemudian cek bagian label. Alpha tergantung yang digunakan dalam contoh ini 1% atau 0.01. Pada Output option terserah teman-teman mau pilih outputnya dimana. Setelah itu pilih ok. maka akan muncul output seperti berikut.
   

Intrepretasi Output anova Excel

Summary

Pada bagian tersebut menyajikan deskripsi dari tiap kelompok baik kelompok umur(baris) dan kelompok metode (kolom). deskripsinya yaitu Banyaknya data(count), Jumlah total(Sum), Rata-rata (average) dan standar deviasi (variance). Untuk penjelasannya bisa diintrepretasikan hasil tersebut karena udah pada ngerti semua lah yaa.

Anova

Bagian ini menampilkan tabel anova seperti pada materi anova satu arah. yang perlu dilihat pada bagian ini adalah P value. jika nilai p value lebih besar dari 0.01(alpha) maka keputusan terima H0 artinya tidak ada perbedaan rata-rata tiap kelompok. Selain itu bisa dilihat dengan membandingkan nilai F hitung (F) dengan F tabel (F crit). terlihat bahwa F hitung lebih kecil dari f tabel maka keputusan sama yaitu terima H0. Sehingga dapat disimpulkan setiap metode dan kelompok umur memberikan rata-rata penurunan berat badan yang sama. Selain itu hasil yang diperoleh hampir sama dengan penyelasian secara manual mungkin beda karena  pembulatan.

[Video Youtube] Anova dua arah tanpa interaksi (two way without interaction)