Uji T berpasangan merupakan salah satu uji hipotesis komparatif untuk dua data berkelompok. selain itu, uji ini juga merupakan uji untuk statistik parametrik dengan syarat merupakan variabel numerik dan berdistribusi normal. apabila syarat tersebut tidak terpenuhi maka menggunakan statistik non parametrik. untuk kasus uji T berpasangan menggunakan uji wilcoxon apabila datanya tidak berdistribusi normal yang mana menggunakan statistik non-parametrik.

Contoh Kasus Uji T berpasangan 2 kelompok
Suatu penelitian dilakukan untuk menguji perbedaan stress kerja karyawan yang bekerja di ruangan yang bersifat tradisional lalu pendah pada ruangan yang modern.
Apakah terdapat perbedaan stres karyaman ketika berada di ruangan tradisional dengan ketika berada diruangan modern?
langkah-langkah melakukan uji T berpasangan:
- Memeriksa syarat uji t untuk kelompok berpasangan:
- Sebaran data harus normal
- varians data tidak perlu diuji karena kelompok data berpasangan
- Jika memenuhi syarat (sebaran data normal), maka dipilih uji t berpasangan.
- Jika tidak memenuhi syarat (sebaran data tidak normal) dilakukan terlebih dahulu transformasi data.
- Jika variabel baru hasil transformasi mempunyai sebaran data yang normal, maka dipakai uji t berpasangan
- Jika variabel baru hasil transformasi mempunyai sebaran data yang tidak normal, maka dipilih uji wilcoxon.
Setelah kita memperoleh data dan memasukkan ke dalam SPSS, maka hasilnya sebagai berikut:

Pada tahap pertama memeriksa syarat uji t berpasangan. syaratnya yaitu data harus bersebaran normal sehingga perlu dilakukan uji normalitas. Sesuai dengan langkah-langkah uji normalitas diperoleh hasil (untuk belum tahu bisa lihat pada postingan sebelumnya[TUTORIAL] Uji normalitas dengan SPSS)

Karena syarat data berdistribusi normal terpenuhi, maka uji hipotesis yang dipergunakan adalah uji t berpasangan.
Langkah-langkah uji t berpasangan:
- Analyze, kemudian compare means....Paired sample t
- Masukkan kedua variabel kedalam kotak paired variables. seperti gambar berikut.

- kemudian continue...ok...Hasilnya sebagai berikut
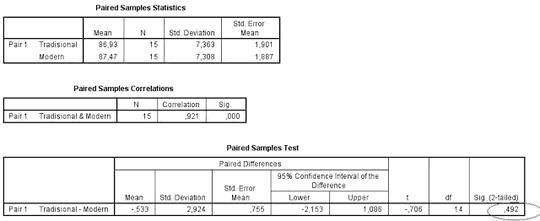
Intrepretasi hasil uji t berpasangan:
1. Bagian paired samples statistics menggambarkan deskripsi masing-masing variabel.
2. Bagian paired samples correlation menunjukkan korelasi antara dua variabel. Tampak korelasi kuat(0,921) dan signifikan (sig=0,000). Salah satu syarat uji t berpasangan adalah kedua kelompok data saling berkorelasi tinggi (r>0,9)
3. Tabel ke tiga Paired Sample Test menggambarkan hasil uji t berpasangan. Lihat kolom sig.(2 tailed). diperoleh nilai significancy 0,492(p>0,05), artinya "tidak ada perbedaan rerata stres karyawan yang berada pada ruang tradisional dengan berapa pada ruang modern".
Untuk materi tentang Pengujian Perbedaan Rata‐rata Dua kelompok berpasangan (dependent) parametrik silahkan klik link tersebut.
Untuk Bisa membandingkan dengan software yang lain silahkan kesini:
[Tutorial Excel] uji t Perbedaan Rata‐rata Dua kelompok berpasangan (dependent) parametrik
Referensi:
Statistik Untuk Kedokteran dan Kesehatan.
Diklat Khusus SPSS, Universitas Gunadarma.
Statistik Untuk Kedokteran dan Kesehatan.
Diklat Khusus SPSS, Universitas Gunadarma.
![[Tutorial SPSS] uji t: Perbedaan Rata‐rata Dua sampel saling bebas (two sample for means) [Tutorial SPSS] uji t: Perbedaan Rata‐rata Dua sampel saling bebas (two sample for means)](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh7Cmka3-Mvi1kMs8J53_ani4Y6uQ0cprExyAf9es39CQlukGqlU_aF6YFOGTLZUZzLj_tDIf1y4dxO3XmX0CmCOMUxp7WvHrcY5SBzA1KJiDsJ0mEVqg0THs39R4lCaaMOLlldS_kNnssw/w72-c-h72/Data+spss.png)
![[Tutorial] Contoh Analisis Regresi Logistik biner/dikotomi dengan SPSS [Tutorial] Contoh Analisis Regresi Logistik biner/dikotomi dengan SPSS](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjAWGKqksUDiFCrtErbEq1nAitVE9nZZRkLzWw3vP4b_JHze8ULIBFc18FkNTlXhXbYAlJkaNjbTSekMAy044qMrIl_fsHGdEctc2Nrd8JCnP06vzn61n9KV2NGkmF-3VQUxvRF3XUqWogp/w72-c-h72/choose+logistic+regression.png)

![[TUTORIAL] contoh kasus analisis faktor dengan SPSS [TUTORIAL] contoh kasus analisis faktor dengan SPSS](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj9xlJ1RTaKHXpa6VpSLBWKWeKyUs-b-5muTwLQqxuwifaXM_SdSf7bwAZuSSRBQbBE4ajxB4DoYfsAY6uNJrkxp-Ja10R9hsfmget8ob4N1_T0TmHdmKzmy78kxJbKeeWtmhkQ2E00HwE9/w72-c-h72/data+lengkap.png)





bagaimana jika salah satu uji normalitasnya tidak normal?
ReplyDeletedianggap normal atau tidak?
harus normal untuk uji berpasangan.
Deletekalau tidak normal pakai metode non parametrik.
untuk uji t berpasangan 2 kelompok meode alternatifnya wilcoxon. tapi kalau datanya bukan numerik pakai mcnamer. sperti pada gambar di atas. disitu bisa dilihat penjelasannya.
itu korelasinya harus >0.9 atau harus signifikansinya <0,05?
ReplyDeleteThanks a lot.
ReplyDeletevarians data tidak perlu diuji karena kelompok data berpasangan. Maaf tolong bisa dijelaskan ?
ReplyDeleteTerima kasih pencerahannya,
ReplyDeleteSalam Blogger
www.sangpengajar.com
kalau untuk menarik kesimpulan terkait hipotesis yang satu arah, nilai mana yang perlu diperhatikan ? apakah cukup dengan nilai p nya saja dan lihat beda meannya, apakah lebih kecil atau lebih besar, atau ada hal lain ?
ReplyDeletemisal Miu nol nya bukan sama dengan 0 gantinya gmn?
ReplyDeleteMisal memiliki perbedaan minimal 2 poin... berarti kan miu nol nya sama dengan 2
untuk sebaran data tidak normal setelah di transform kita pakai data awal atau data transform?
ReplyDeletekalau tidak normal, apakah harus memakai median, bukan mean?
This is the precise weblog for anybody UN agency must search out out concerning this subject. You notice such a lot its nearly arduous to argue with you. You completely place a spanking new spin on a topic that is been written concerning for years. Nice stuff, merely nice!
ReplyDeleteApakah ada kemungkinan nilai sig data t tes berpasangan menerima H0,sedangkan mean post tes lebih besar nilainya. Terimakasih.
ReplyDelete